Dans l'article précédent, nous avons

• présenté le cadre théorique de l'ACV : fonction, système, étapes du cycle de vie
• décrit en quoi consiste la modélisation en ACV
• touché du doigt la difficulté de calculer l'impact total sur l'environnement à partir d'un modèle ACV

Nous présentons ici comment aborder ce calcul.

Exemple

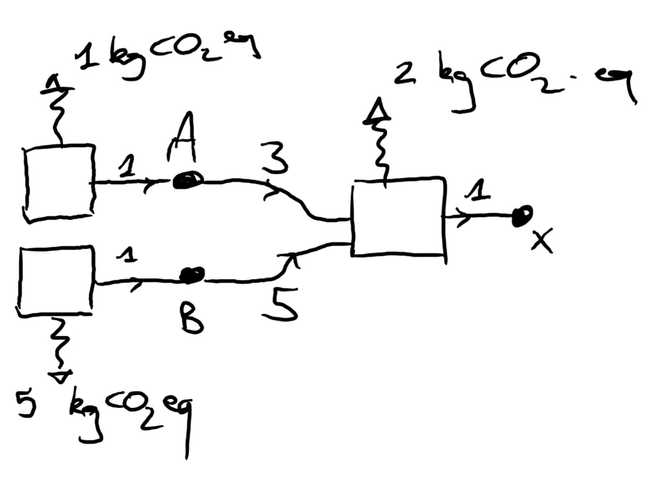
Reprenons un exemple simple.

Nous avons

• trois produits $X$, $A$, et $B$
• trois processus (les boîtes), que nous nommerons, pour simplifier, par l'unique produit qu'ils produisent : $X$, $A$ et $B$.
• chaque processus $p$ émet (unitairement) directement dans l'environnement une quantité $\iota_p$ de CO2-eq

Et nous cherchons à calculer l'impact total $\phi_X$ (en kg CO2-eq) de la production d'une unité de $X$. Pour cela, il est utile d'introduire également :

• $\phi_A$, impact total de la production d'une unité de $A$
• $\phi_B$, impact total de la production d'une unité de $B$

En se rappelant l'hypothèse fondamentale de linéarité des processus unitaires, nous interprétons le graphe de la manière suivante

• 1 unité de A émet directement 1 kg CO2-eq
• 1 unité de B émet directement 5 kg CO2-eq
• 1 unité de X
  • requiert 3 unités de A, soit $3 \cdot 1 = 3$ kg CO2-eq
  • requiert 5 unités de B, soit $5 \cdot 5 = 25$ kg CO2-eq
  • émet directement 2 kg CO2-eq

L'impact total est donc $2 + 5 + 3 = 10$ kg CO2-eq. Cela se traduit en équation

Dans ce cas simple, on le résoud directement

Reformulation

Linéarité des processus unitaires

On peut reformuler la section précédente dans le cadre un petit peu plus général des processus à $n$ sorties et $m$ entrées. En effet, un tel processus $p$ se caractérise par

• pour chaque sortie $o$ du processus, une quantité $q_o$ d'unités de produit $o$
• pour chaque entrée $i$ du processus, une quantité $q_i$ d'unités de produit $i$
• des émissions directes dans l'environnement associées à l'exécution du processus $p$, que l'on résume ici par un unique nombre $\iota_p$

L'hypothèse fondamentale de linéarité prend la forme suivante

ou encore

Forme matricielle

En notant $\phi$ le vecteur (colonne) des $\phi_x$ pour tous les produits $x$, $\iota$ le vecteur (colonne) des $\iota_p$ pour tous les processus $p$, on peut résumer ce système d'équations linéaires par une équation matricielle

où $\nabla$ (prononcer nabla) est une matrice indexée en ligne par les processus $p$, en colonne par les produits $x$, et définie par

La matrice $\nabla$ caractérise complètement le modèle. Elle est connue, en théorie des (hyper) graphes, comme la matrice d'incidence associée au (hyper) graphe du modèle.

Calculs des impacts totaux par inversion

Le calcul des impacts totaux pour chacun des produits se fait alors en inversant la matrice $\nabla$

Noter que la matrice $\nabla$ n'est pas toujours inversible (par exemple, lorsqu'elle n'est pas carrée). Il est remarquable de constater que la non-inversibilité de la matrice se résout généralement par des décisions méthodologiques non triviales.

Il y a plus de processus $p$ que de produits $x$ : processus de marché

Cela arrive lorsque, par exemple, deux processus $p$ et $q$ produisent un même produit $x$. On peut imaginer par exemple que l'électricité (produit $x$) puisse provenir d'une centrale nucléaire (processus $p$) ou d'une centrale thermique ( processus $q$).

Pour éviter cet écueil, il est d'usage de modifier le modèle en remplaçant le produit $x$ par :

• un produit $x_p$ spécifique "électricité de la centrale nucléaire", produit uniquement par le processus "centrale nucléaire" $p$
• un produit $x_q$ spécifique "électricité de la centrale thermique", produit uniquement par le processus "centrale thermique" $q$
• un processus "marché de l'électricité" $m$
  • qui a pour seul produit, le produit "électricité" $x$
  • qui a pour entrées les produits "électricité de la centrale nucléaire" et "électricité de la centrale thermique"

Noter qu'il y a une décision de modélisation à prendre ici. En effet, l'analyste doit choisir des coefficients pour les entrées du processus "marché de l'électricité". C'est, d'une certaine manière, cette ambiguïté qui empêche la première matrice d'être inversible.

Il y a plus de produits $x$ que de processus $p$ : allocation

Cela arrive lorsque, par exemple, un processus $p$ a deux produits $x$ et $y$ en sortie. Ainsi, le processus $p$ de "transformation de vache" peut avoir du "lait" $x$ et de la "viande" $y$ en sortie.

Dans ce cas, on modifie le modèle en remplaçant le processus $p$ par :

• un processus $p_x$ "transformation de vache pour faire du lait" qui est le seul processus produisant du "lait" $x$, avec les mêmes entrées que le processus $p$
• un processus $p_y$ "transformation de vache pour faire de la viande" qui est le seul processus produisant de la " viande" $y$, avec les mêmes entrées que le processus $p$
• un choix d'une allocation de l'émission directe $\iota_p$ pour chacun des processus $p_x$ et $p_y$ : quelle proportion de l'émission directe $\iota_p$ de $p$ est attribuée respectivement à $p_x$ et $p_y$ ?

Encore une fois, le dernier point une décision de modélisation à prendre. Lors de la transformation "physique" d'une vache en lait et viande, quelle part revient au lait ? quelle part revient à la viande ? C'est cette nouvelle ambiguïté qui empêche la première matrice d'être inversible.

Le modèle contient des boucles divergentes

La formulation matricielle a l'avantage de s'accommoder très simplement des boucles : en effet, rien n'empêche le modèle de contenir des boucles tant que la matrice $L$ est inversible. Mais il est simple d'imaginer un cas où une boucle empêche l'inversion :

• un processus $p$ produit une unité de $x$ en consommant une unité de $y$
• un processus $q$ produit une unité de $y$ en consommant une unité de $x$

Alors $\nabla = \begin{pmatrix} 1 & -1 \\ -1 & 1 \end{pmatrix}$, qui n'est pas inversible (déterminant nul). D'une certaine manière on conçoit, sur cet exemple, que "rien ne diminue lorsqu'on tourne sur la boucle".

Par contre, il suffit d'"atténuer à chaque passage de la boucle" pour s'en sortir

• un processus $p$ produit une unité de $x$ en consommant une unité de $y$
• un processus $q$ produit une unité de $y$ en consommant une demi-unité de $x$

Alors $\nabla = \begin{pmatrix} 1 & -0.5 \\ -1 & 1 \end{pmatrix}$, qui est inversible.

Remarques finales

Nous avons considéré l'impact total $\phi_x$ d'un produit $x$ comme un scalaire, par exemple, une quantité de kg CO2-eq. Il est bien sûr possible de reformuler l'ensemble de l'article dans le cas où $\phi_x$ est, entre autres, un vecteur dont chaque entrée correspondrait à un type de substance émise dans l'environnement, ou bien un indicateur ACV classique (changement climatique, déforestation, etc.). Cela complique le nombre de dimensions, mais ne change rien aux principes.

Conclusion

Nous avons, dans cet article :

• introduit une représentation matricielle $\nabla$ d'un modèle ACV, qui n'est autre que la matrice d'incidence associé au (hyper) graphe du modèle.
• dérivé l'équation fondamentale de l'ACV

• lié les conditions d'inversibilité de la matrice $\nabla$ à trois opérations méthodologiques
  • l'introduction de processus de marché
  • l'allocation d'émissions directes à plusieurs processus assimilés
  • l'atténuation de boucles divergentes

Il y a sans doute beaucoup à dire encore sur les mathématiques de l'ACV

• relations entre la modélisation en ACV et la modélisation Walrassienne (théorie de l'équilibre générale).
• analogie avec la théorie du potentiel ($\phi$) et courant ($\iota$), $\nabla$ jouant le rôle d'une dérivation.
• cas de coefficients stochastiques dans la matrice $\nabla$ ou le vecteur $\iota$, par exemple, pour modéliser les incertitudes.

Choses que l'on réserve pour de futurs articles.